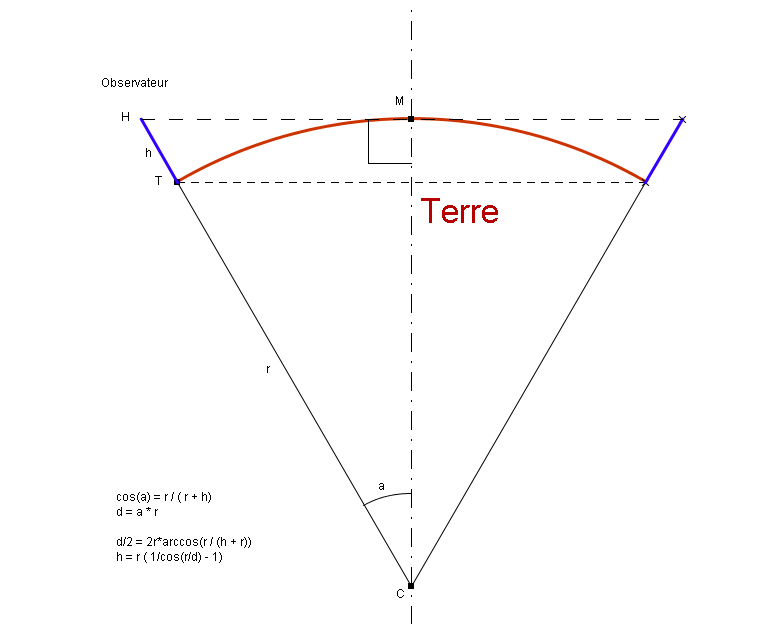
Rien de tel que des vacances à la mer pour observer la rotondité de la terre. En effet, pour un homme de 2 mètres de haut, l’horizon est à 5km. Cela signifie qu’il pourra voir un bateau de sa taille jusqu’à 10km, ou un cargo de 20 mètres de haut jusqu’à 25km de distance, ou une ile de 100m jusqu’à 40km !