MarEtud – Prévision des Marées (TIPE)

En classes préparatoire, une des épreuves des concours est un TIPE (Travail d’Initiative Personnelle Encadrée). Ce TIPE a pour objectif de nous faire travailler sur un sujet que l’on choisit (dans le thème “Terre et Espace”), et que l’on aura à présenter à un jury. Comme projet j’ai choisi l’étude des Marées et leur prédiction.

Dans le cadre de ce projet, j’ai réalisé un programme qui permet :

1. de prédire les marées, la hauteur d’eau ou les horaires pour un lieu déterminé,
2. de déterminer les constantes nécessaires au calcul, pour que ce programme soit utilisable par tous.

Documents TIPE : Fiche synoptique, Présentation.

Le logiciel utilisé est plutôt ancien (initialement prévu pour Win 3.1). Vous pouvez le télécharger ci-dessous, mais si seule la partie prédiction vous intéresse, les programmes basés sur XTide devrait répondre à vos attentes.

MarEtud

MarEtud est un logiciel spécialement prévu pour comprendre la prédiction des marées, et de la faire soi-même pas à pas. Ce logiciel vous permettra ainsi de faire des prédictions de marées à partir d’ondes harmoniques (un peu comme tous les logiciels qui font ça bien mieux), mais également de pouvoir calculer ces harmoniques, et comprendre comment cela fonctionne.

Télécharger MarEtud

Programme : maretud.zip : contient le programme, son fichier d’aide, et les sources. Les sources sont uniquement destinées à un usage informatif.

Données de ports Français pour XTide : Attention, ces données sont très anciennes et visiblement peu fiables. xtide_france à ajouter à un fichier harmonics.txt compatible (attention, format très ancien !)

Le SHOM permet d’obtenir des fichiers de relevés de hauteur d’eau nécessaires à la détermination des constantes harmoniques.

Fonctions de visualisation de la marée

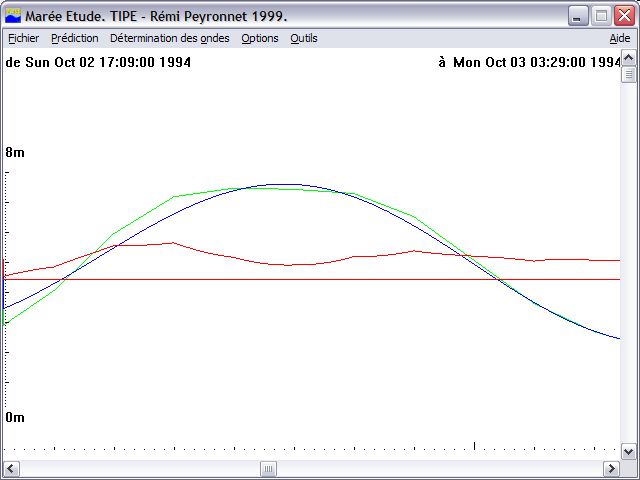
Le logiciel permet de regarder simultanément l’enregistrement des hauteurs d’eau, et la marée prédite. Cela permet de comparer facilement les deux résultats, et pouvoir observer et comprendre les différences (météo, tenue du plein, …)

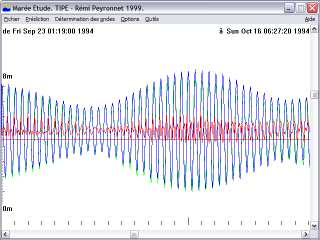
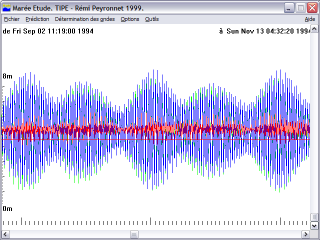
Une autre fonctionnalité intéressante est celle de pouvoir faire facilement changer l’échelle d’affichage, à l’aide de la barre de défilement de droite. Une vision sur un mois met ainsi en évidence l’importance des phases de la lune, et sur plusieurs mois, montre que cela n’est pas la seule variable.

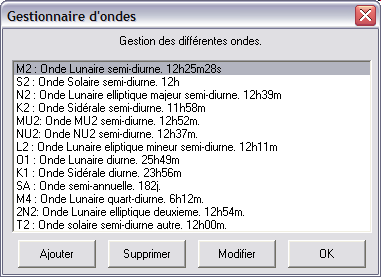
Fonctions de détermination de nouvelles périodes

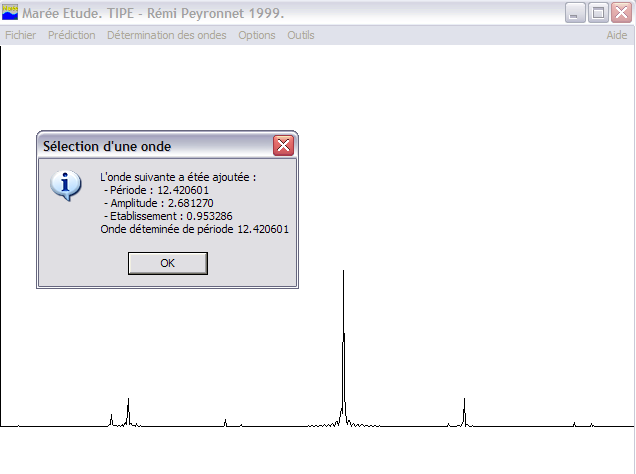
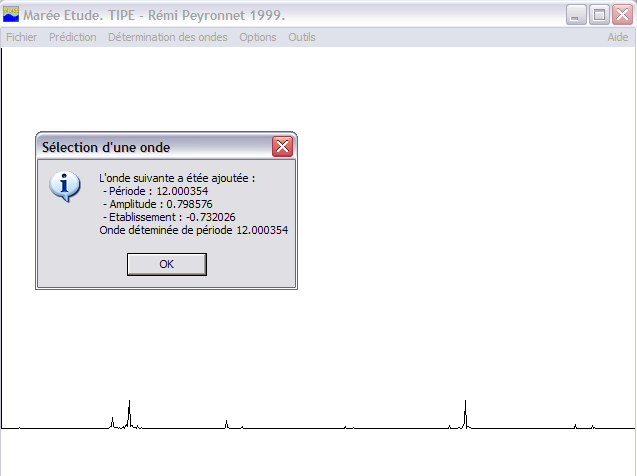
Le logiciel propose également de déterminer les variables harmoniques à l’aide de périodes pré-enregistrées. Mais il propose également un moyen intéressant de détermination des ondes harmoniques expérimental, par balayage du spectre, et détermination de l’onde maximum. Cette onde est ensuite retirée, et le processus est itéré. Nous pouvons constater qu’en usant de ce procédé, le pic de l’onde semi-diurne est correctement repéré, puis disparait complètement lorsque cette seule onde est enlevée (cf “Tentative FFT” pour une idée de méthode directe, mais qui ne fonctionne pas). La méthode est longue (environ 2mn par itération sur une machine 2GHz pour traiter un fichier d’une dizaine d’années), mais efficace (dans une démarche expérimentale, sinon utilisez les valeurs pré-enregistrées :-).

Fonctions plus classiques

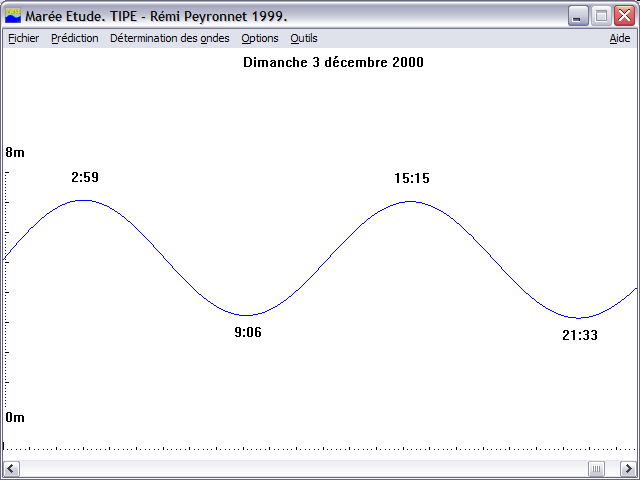
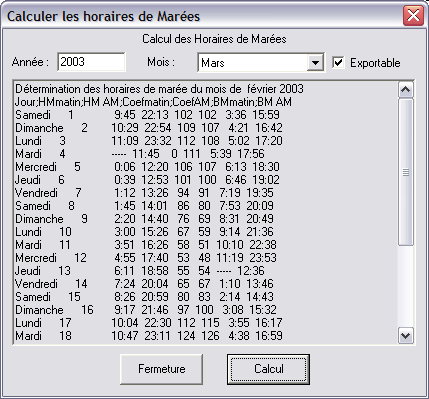
Le logiciel propose également un écran de prédiction pour les jours futurs (le but ultime de tout ça en fait :-), ainsi qu’une possibilité de génération des tables horaires (exportable dans un tableur pour peaufiner un peu la mise en page).

Tentative d’une méthode directe utilisant la FFT

Pouquoi ?

Le processus itératif décrit plus haut est bien, mais lent : il faut balayer de manière assez fine tout le spectre, pour pouvoir trouver quelquechose, et dès que la quantité de données augmente, les temps de calculs deviennent de plus en plus longs (en O(n)).

Pourtant, cette détermination automatique est intéressante, d’une part parceque l’on ne connait pas forcément toutes les périodes cosmiques et leur harmoniques qui peuvent rentrer en jeu, mais il peut s’y ajouter d’autre phénomènes, de type résonnance, météo cyclique,…

L’idée de base

L’idée de base est de se dire que les points résultants de la FFT sont globalement situés sur une courbe assimilable au sinus cardinal que l’on obtient en transformée de Fourier classique (le processus utilisé dans MarEtud). Or nous connaissons parfaitement l’équation du sinus cardinal ( sinc(x) = sin(x)/x ).

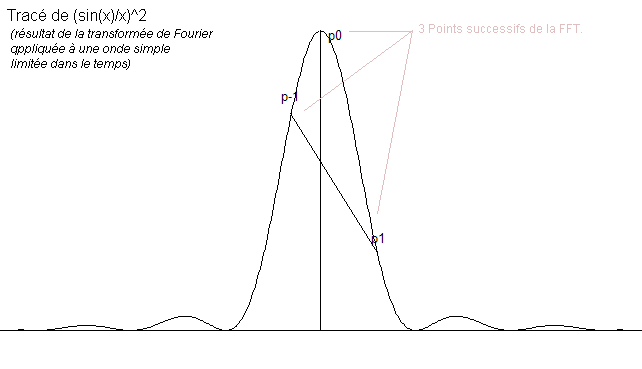
Nommons p0 le point d’intensité maximum détecté par la FFT, et p-1, p1 les deux points strictement avant et après ce point. En supposant que ces deux points sont situés sur le même lobe (et c’est justement la le hic), alors il est possible de remonter directement à la coordonnée du centre du lobe. Grace à l’étendue temporelle de nos enregistrements, nous connaissons la largeur d’un lobe. Par contre, nous ne connaissons pas son hauteur. Pour s’affranchir de cette hauteur, nous allons faire le rapport de la hauteur de p-1 et p1, que nous noterons ‘r’. J’ai préféré prendre p-1 et p1 pour des raisons de symétries, mais rien n’empeche de prendre p0. En ayant normé notre fonction suivant x et y, nous sommes capable de la confronter à la théorie.

Il ne nous reste plus qu’à résoudre l’équation r = h(x), avec h(x) = sinc(x+1)/sinc(x-1). Cette equation est assez simple a résoudre, car la courbe est relativement linéaire, et très bien approchée par un polynôme de degré 3. La valeur de x nous donnera la coordonnées de p0 par rapport à l’origine locale du lobe. Et nous avons alors exactement ce que nous voulons : l’emplacement aussi précis que nous le voulons (par la précision de la résolution de l’équation r = h(x) ), quasi directement après une FFT.

Pourquoi cela ne marche pas

C’est très simple, le pré-requis d’avoir plusieurs points de FFT sur un lobe n’est pas rempli. Voici un simple graphique Excel pour s’en convaincre :

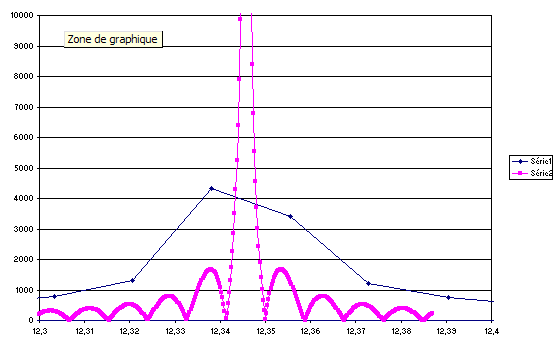
On retrouve naturellement ce résultat par le calcul (on trouve en fait qu’il y a une mesure de FFT pour PI lobes du sinus cardinal, et non pas PI mesures pour un lobe, comme j’avais trouvé avant de me lancer la dedans 🙂

Plus d’information ?

J’ai écrit quelques programmes et scripts Scilab pour tester la faisabilité du procédé. Comme cela n’a pas abouti, je n’ai pas jugé bon de les mettre à disposition, mais si cela vous intéresse, il vous suffit de m’écrire un mail.